Annual report 2018

A new scaling method for the acoustic design of transmission size ranges.

Scaling laws, acoustics, transmission size range

Transmission size ranges contribute to the flexible use of drive technology systems and make product development more cost-effective by exploiting similitude. So far, the acoustic design of transmission size ranges has been characterized by the fact that each size of a transmission size range is analyzed separately, resulting in increased effort in numerical and experimental simulation.

Darmstadt scientists are developing methods that can be used to scale results from numerical and experimental simulations from one size to another. The goal is to form a reliable prognosis of acoustic behavior while reducing the time requirement.

Scaling laws can predict the acoustic behavior of an original structure (such as a transmission) using a scaled structure by exploiting the similitude between the original structure and the scaled structure. For example, results from experimental simulations of a particular size of a transmission housing can be scaled to other sizes of similar transmission housing. The idea here is more about a reliable prognosis of the acoustic behavior than about its exact prediction, so that the time requirement can be reduced, especially in experimental simulations. Currently, scaling laws are still derived manually, which is not financially viable in industrial practice.

Therefore, scaling laws are still not applied to the acoustic design of transmission size ranges. The Department of System Reliability, Adaptive Structures, and Machine Acoustics SAM of Technische Universität Darmstadt is developing and validating a more efficient scaling method for the acoustic design of transmissionsize ranges.

Derivation of scaling laws through numerical simulation

The new scaling method combines previous scaling methods based on the similitude theory with sensitivity analyses, so that the scaling laws can no longer be derived manually, but rather automatically. The scaling laws are the result of power products whose exponents are calculated through sensitivity analysis. For example, this allows scaling laws to be derived directly from numerical simulations, which significantly reduces the time required to derive scaling laws. The derivation of scaling laws thus becomes significantly more efficient and can potentially become more significant in industrial practice.

Numerical validation of the scaling laws

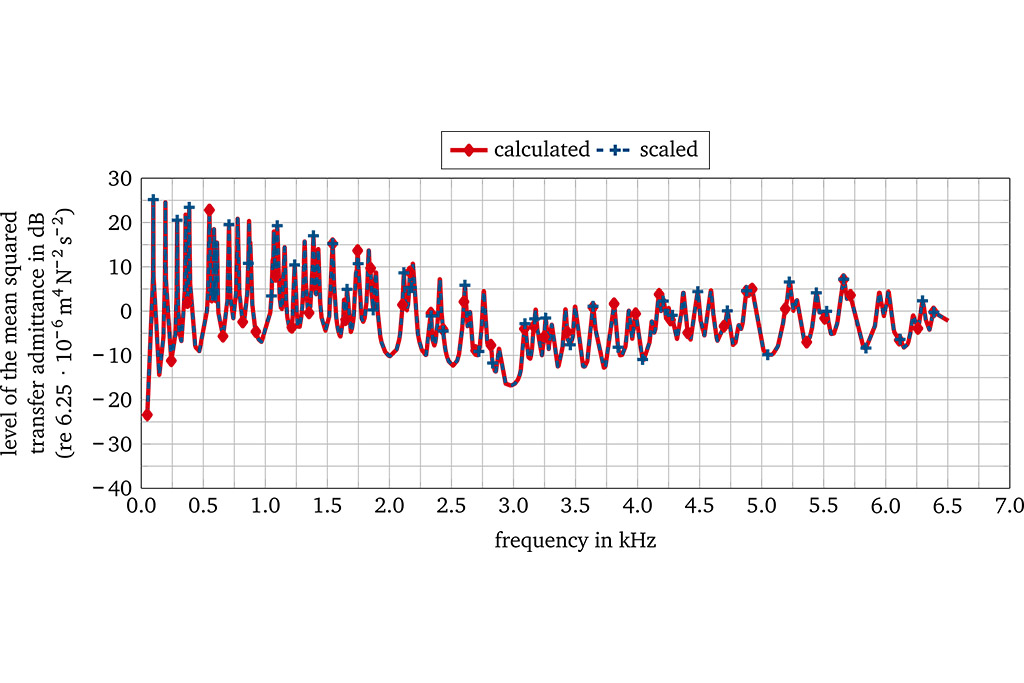
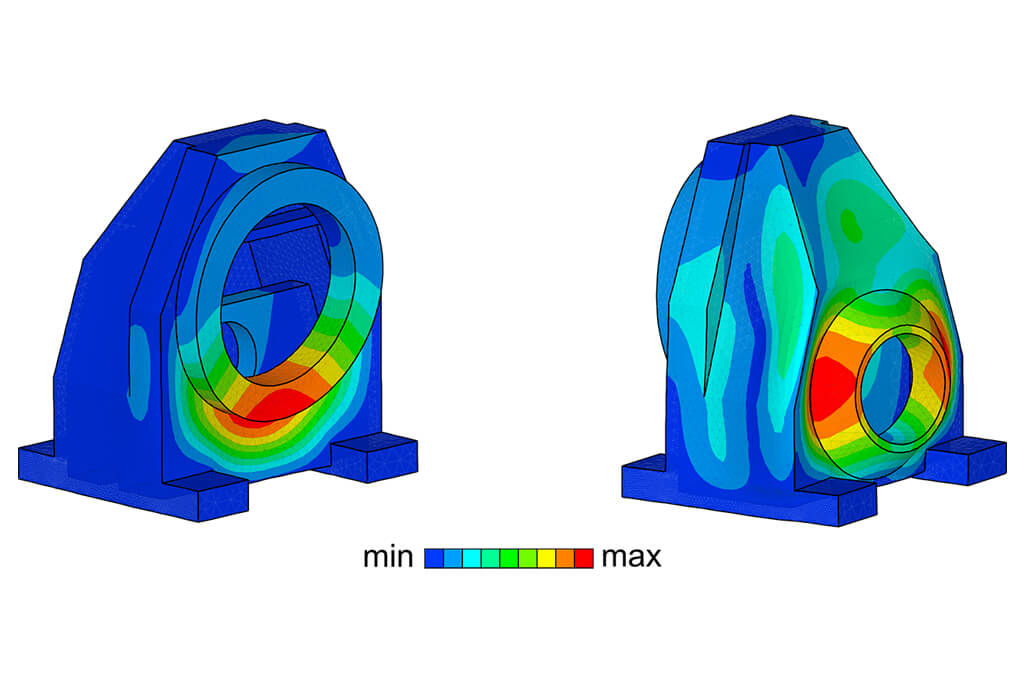
The scaling laws are initially derived for simple plate structures and verified using existing scaling laws from literature. Numerical calculations of scaled rectangular plates and plate-like structures show that typical acoustic responses (such as natural frequencies, mean squared transfer admittance or local vibration velocities) can be transferred from a structure to a scaled structure with high accuracy using the newly developed scaling method (Fig. 2). By combining finite element calculations with a local sensitivity analysis, this transmission size range example illustrates that the scaling behavior of the natural frequencies is mostly determined by those geometry design parameters that most affect the natural frequencies. This is mainly due to the vibration behavior of the transmission housing, which is mainly characterized by local vibration modes (Fig. 3).

Experimental validation of the scaling laws

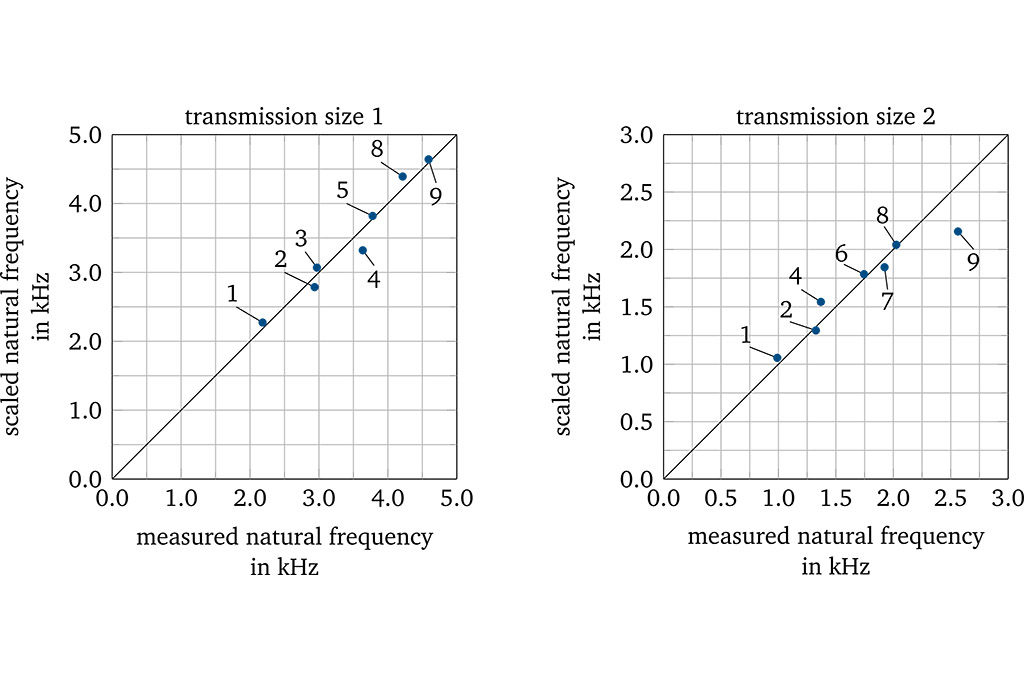
Experimental studies have also shown that the measured natural frequencies of a transmission size range can be scaled using the new scaling method. The challenging part lies in the fact that the natural vibration modes change depending on the size, meaning that scaling of natural frequencies is more demanding.

Nonetheless, the natural frequencies of the transmission size range can be scaled with a sufficient accuracy (Fig. 4). Hence, the developed scaling method can also be used efficiently in industrial practice.